Estimating the reduction in cost-per-game in production runs

Listening to the GTS lectures over the past couple of days, I've learned that part of the reason prices drop so precipitously with increased numbers of games printed is that the presses churn out a bunch of games before the colors and print quality are set correctly.  The number referenced by Dan Tibbles in the lectures is 1,000 games printed and discarded before they can start the actual print run.  That seems like a fantastically high number, but I know very little about commercial printing, so I'll certainly accept it until I learn otherwise.

I thought I'd compare the production prices for one of my printing bids to this model, where 1,000 games are wasted.  What that means is if you're ordering 1,000 games, you're actually paying for 2,000, so your cost of production should be double what it actually is per game.  If you order 2,000 games, you're paying for 3,000 copies, so your costs are 150% of the actual cost.  The more you order, the more your cost drops, because the wasted games become less and less of the total produced, and their costs are pro-rated over the whole print run.

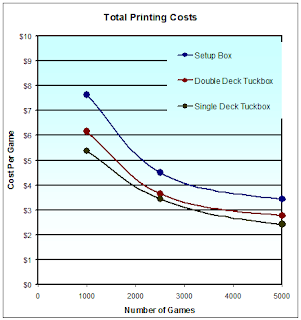
Sounds reasonable, right?  Well, I thought I'd test it out to see what's going on.  Here's an actual bid on my game from Imagigrafx.  If you're interested, I discussed this in more detail in an earlier post here.

You can clearly see the drop in cost per game with increasing production runs.

I thought I'd try to model this statistically.  The bid above tapers off to something near $2 per game.  So, here's a hypothetical print run, for a game that costs $2 per game to print, but with 1,000 wasted games that also cost $2 per game.  So, if you print 1000 and waste 1000, it will end up costing you 2,000 * $2 = $4,000.  But, you only get 1,000 games, so that comes out to an apparent cost per game of $4.

This graph has the same shape as the real offer above, which makes sense.  However, the values don't line up quite right - the drop off is steeper here, and you approach the $2 more quickly than in my real data.  

So, this model doesn't quite work.  I tried it out with 2,000 wasted games, and it was much closer (green line below):

So, is that's what's happening? 2,000 wasted games?  Probably not, in reality.  I'd guess there are a bunch of actual sunk costs to setting up a print run, and those are going to have to be paid regardless of the size of the run.  So rather than wasting 2,000 games, it might be much fewer, and instead, the sunk costs (one-time setup costs) are making up the rest of the elevated apparent cost per game.

But as far as the statistics go, 2,000 wasted games seems to model the real bid I was getting pretty well, even if it's not exactly what's happening.  Maybe this is a good rule of thumb in estimating the drop-off in printing costs for extended print runs?  Seems like an easy enough model to use.